
猫吧学习社吧 关注:307贴子:3,691
- 33回复贴,共1页
本人方法是先画出两个高的交点,在证明另一个定点于此交点的连线垂直于此定点的对边,若垂直,由于过一点有且只有一条直线与已知直线垂直,所以三条高交于一点

如图:BE垂直于AC CF垂直于AB并与BE交于O,证明AO垂直于BC
连接FE(刚刚作图忘连了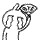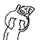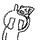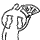 )
)
∵BE垂直于AC CF垂直于AB
∴△AOF和△AOE是直角三角形
又∵△AOF和△AOE共斜边
∴AFOE在同一圆内
∴∠FAO=∠FEO(∠FEB)
同理∵△BCF和△BCE共斜边
∴∠FAO=∠FEB=∠FCB
∵∠FAO+∠FOA=90° ∠FOA=∠COD
∴∠FCB+∠COD=90°
∴AD垂直于BC
证明完毕

如图:BE垂直于AC CF垂直于AB并与BE交于O,证明AO垂直于BC
连接FE(刚刚作图忘连了
∵BE垂直于AC CF垂直于AB
∴△AOF和△AOE是直角三角形
又∵△AOF和△AOE共斜边
∴AFOE在同一圆内
∴∠FAO=∠FEO(∠FEB)
同理∵△BCF和△BCE共斜边
∴∠FAO=∠FEB=∠FCB
∵∠FAO+∠FOA=90° ∠FOA=∠COD
∴∠FCB+∠COD=90°
∴AD垂直于BC
证明完毕

至于我楼常用的四点共圆:
题设:当两个三角形共斜边时
结论:他们的四个顶点在同一圆上
至于证明取那个公用斜边的中点,很容易知道斜边上的两个点距此点一半的距离,另外两个点相聚的距离也是这个长度,这个简述的证明大家都能明白吧,(不上图了,几何画板画的太慢
题设:当两个三角形共斜边时
结论:他们的四个顶点在同一圆上
至于证明取那个公用斜边的中点,很容易知道斜边上的两个点距此点一半的距离,另外两个点相聚的距离也是这个长度,这个简述的证明大家都能明白吧,(不上图了,几何画板画的太慢

扫二维码下载贴吧客户端
下载贴吧APP
看高清直播、视频!
看高清直播、视频!
贴吧热议榜
- 1尹锡悦拒绝提前下台1984500
- 2Yagao疑似退役1820214
- 3iOS18.2正式版发布1424080
- 4尤文2-0送曼城客场7场不胜1106001
- 5这才是虎先锋原本的实力1057914
- 6《守望先锋2》国服疑似回归855875
- 7名嘴称詹姆斯不配与库里同队695640
- 8如何看待年轻人高价买谷613226
- 9LOL黑玫假面系列皮肤公布533126
- 10黑神话联名吧友纷纷询问葫芦464016













