一个简单的例子是足球比赛前Toss-up 抛硬币决定谁先开球，硬币正面和反面出现的概率各为1/2。
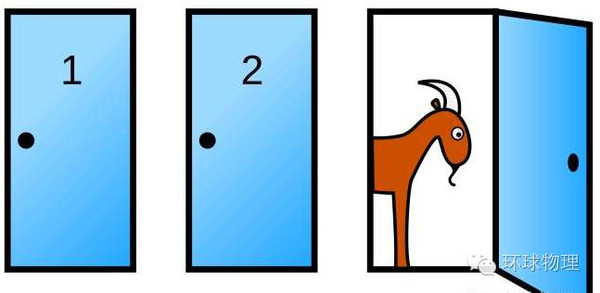
　　你在参加一个节目，面前是三扇关闭着的门。其中一扇后面是小汽车，选中它就可赢得汽车，另外两扇后面各是一只羊。你选择了其中一扇，但没有打开它，这时主持人打开了剩下两扇门中的一扇，后面是一只山羊（这里有个隐含前提：主持人是知道门后的情况的）。主持人问你，要不要换另一扇仍然关闭着的门，还是就要你刚才选中的那扇。
　　那么问题就是，换另一扇门会增加你赢得汽车的概率么？换与不换的概率各是多少呢？
　　
　　。。。。。。
　　答案是---换！
　　不换门的话，赢得汽车的概率是1/3，换门的话，赢得汽车的概率为2/3.
　　还在想why? 呵呵，
　　主持人选择过程是概率重新变换的一个过程。第一次选中的概率是1/3，消去一个错误答案后，如果你的选择不变，概率保持原来的1/3；如果转换，就相当于认为自己选的不是正确的，而上一次选中不正确的概率为2/3。所以，如果转换就是2/3，不转换就是1/3。
　　这个问题亦称之为蒙提霍尔悖论。虽然该问题的答案在逻辑上并不自相矛盾，但十分违反直觉。
　　所以，不要轻信自己的直觉。
　　有时候，我们也要敢于认错。