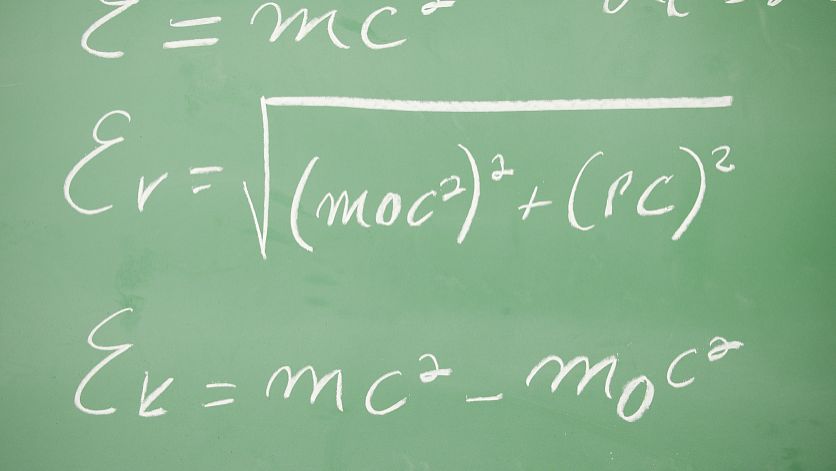Obtain the best least-square approximation to the function sin(πx/2)in the interval -1<=x<=1 using the first 4 Lefendre polynomials. Calculate both the L² and the max norms of the error (within a 5-10% accuracy is enough). Recall that P0=1, P1=x, P2=(3x²-1)/2, P3=(5x²-3x)/2 These are orthogonal, but not orthonormal
数学吧 关注:894,623贴子:8,764,098
- 9回复贴,共1页
扫二维码下载贴吧客户端
下载贴吧APP
看高清直播、视频!
看高清直播、视频!
贴吧热议榜
- 1合租女室友竟是脏脏公主1869270
- 2泽连斯基想找中国当靠山1391014
- 3国家线出了你有学上吗1390676
- 4国家出手治理农村高额彩礼1367766
- 5小行星爽约不撞地球了1282814
- 6原神内鬼吧激烈内斗1090475
- 7BLG淘汰TT完成复仇786720
- 8华为新手机对标迷你折叠平板685170
- 9P社捂嘴中国玩家硬刚到底522676
- 10卡梅隆称阿凡达3为三部曲最佳487725