什么是数组?数组是一系列(同一区域下的)单元格内,确定只能填入某些数字,并且可以换着填都没毛病的结构,严谨来说,数组分两种,显隐性:
显性数组:同一区域下,n个单元格内只有n种不同的数字;
隐性数组:同一区域下,n种不同的数字只能填入到n个单元格内。
不过,在上述叙述之中,“同一区域下的”六个字被打上了引号。也就是说,数组并不只是这么简单的用法。在较难的题目之中,数组并不一定必须要存在于同一区域内。
Part 1 Sue de Coq(SdC)
SdC是一种数独技巧,它是典型的跨区数组结构。我们随意拿出一个示例作为分析。

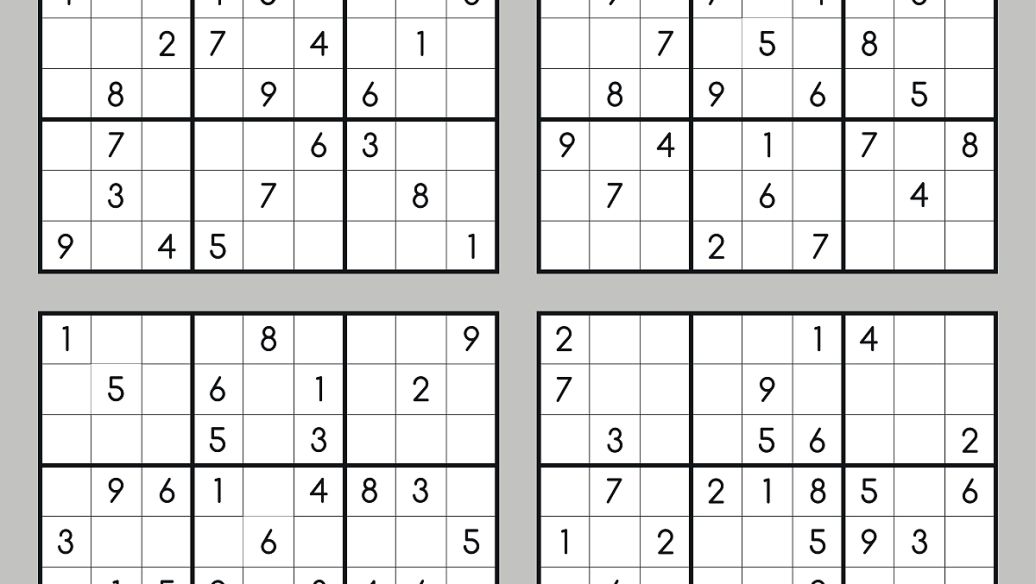
如图所示,紫色的四格里,恰好只有3、4、7、8四种不同的数字。那就一定能够表明,它是一个数组吗?
是不是数组不仅仅只考虑上述定义里的内容,还要思考,里面有没有可能会相同的数字?这是为什么呢?如果这四格里有可能出现相同的数字出现的话,那就最多只可能有三种不同的数字,而占据了四格,那剩下没有出现的数字是我们无法预料到的,推导无法继续进行下去。所以,必须是完全都不同的数字。
幸好,SdC就是这样的一个结构,可以发现,4和7在这个区域下,只有同列出现,而3和8则只在同宫内出现。这样一来,数字就无法出现相同的情况了。
那么不能有相同的数字,也恰好是四个单元格填四种不同的数字,显然是跨区的四数组了。那么,可以遵循数组的方式删数。那怎么删数?我们保证里面的填数一定在其中的,换句话说,3、4、7、8一定会在其中出现,且不可能有多出来的无关数字,也不可能少掉一些完全不出现的数字。所以,大大方方地找到所在区域,删掉即可。例如3和8,由于只出现于结构的同一宫之中,那么该宫内其余位置也就不能是3和8了,删掉它们;同理,4和7也一样。
当然了,SdC是需要结构跨越行宫或列宫两个区域的跨区数组,那行列跨区数组存在么?存在。
Part 2 行列跨区数组

如图所示,题目来自于陆仁贾童鞋在欧泊颗上的标准数独骨灰级PK。
划线处四格只有1、2、7、8四种数字,可能是数组结构。
那么,内部可能不可能有相同数字呢?显然不能。1和7只出现于它们所在列;而2和8也只出现于它们所在行。所以,数字也显然不会产生重复。那,我们可以保证,1、2、7、8一定会出现于其中了。于是可以直接对对应所在行列进行删数。删数我就没画出来了,自己思考。
Part 3 伪数组
要说伪数组这种东西呢,它就不能算是一种跨区数组了,因为它内部完全是可能存在重复数字的,这一点我们无法作出保证,但能够保证的是,内部只会有一种数字有重复,这样便于我们思考问题和得到删数。

喏,这种结构就是一个伪数组,伪五数组。
可以确定里面只有五种数字,也是五个单元格。可以发现,里面数字7可能有重复填写的情况。比如数字可以同时填在F2和E9。
但不论如何,这四个7都不能全部没有。如果全部都消失了的话,五格里就只剩下1、4、5、8四种数字,且不能重复。五格显然是不够只填写四种数字的,所以这样是矛盾的。所以,7是至少有一个了。
那么,这个结构删除的地方,就是所有7的交集。E1就是它们的交集。
显性数组:同一区域下,n个单元格内只有n种不同的数字;
隐性数组:同一区域下,n种不同的数字只能填入到n个单元格内。
不过,在上述叙述之中,“同一区域下的”六个字被打上了引号。也就是说,数组并不只是这么简单的用法。在较难的题目之中,数组并不一定必须要存在于同一区域内。
Part 1 Sue de Coq(SdC)
SdC是一种数独技巧,它是典型的跨区数组结构。我们随意拿出一个示例作为分析。

如图所示,紫色的四格里,恰好只有3、4、7、8四种不同的数字。那就一定能够表明,它是一个数组吗?
是不是数组不仅仅只考虑上述定义里的内容,还要思考,里面有没有可能会相同的数字?这是为什么呢?如果这四格里有可能出现相同的数字出现的话,那就最多只可能有三种不同的数字,而占据了四格,那剩下没有出现的数字是我们无法预料到的,推导无法继续进行下去。所以,必须是完全都不同的数字。
幸好,SdC就是这样的一个结构,可以发现,4和7在这个区域下,只有同列出现,而3和8则只在同宫内出现。这样一来,数字就无法出现相同的情况了。
那么不能有相同的数字,也恰好是四个单元格填四种不同的数字,显然是跨区的四数组了。那么,可以遵循数组的方式删数。那怎么删数?我们保证里面的填数一定在其中的,换句话说,3、4、7、8一定会在其中出现,且不可能有多出来的无关数字,也不可能少掉一些完全不出现的数字。所以,大大方方地找到所在区域,删掉即可。例如3和8,由于只出现于结构的同一宫之中,那么该宫内其余位置也就不能是3和8了,删掉它们;同理,4和7也一样。
当然了,SdC是需要结构跨越行宫或列宫两个区域的跨区数组,那行列跨区数组存在么?存在。
Part 2 行列跨区数组

如图所示,题目来自于陆仁贾童鞋在欧泊颗上的标准数独骨灰级PK。
划线处四格只有1、2、7、8四种数字,可能是数组结构。
那么,内部可能不可能有相同数字呢?显然不能。1和7只出现于它们所在列;而2和8也只出现于它们所在行。所以,数字也显然不会产生重复。那,我们可以保证,1、2、7、8一定会出现于其中了。于是可以直接对对应所在行列进行删数。删数我就没画出来了,自己思考。
Part 3 伪数组
要说伪数组这种东西呢,它就不能算是一种跨区数组了,因为它内部完全是可能存在重复数字的,这一点我们无法作出保证,但能够保证的是,内部只会有一种数字有重复,这样便于我们思考问题和得到删数。

喏,这种结构就是一个伪数组,伪五数组。
可以确定里面只有五种数字,也是五个单元格。可以发现,里面数字7可能有重复填写的情况。比如数字可以同时填在F2和E9。
但不论如何,这四个7都不能全部没有。如果全部都消失了的话,五格里就只剩下1、4、5、8四种数字,且不能重复。五格显然是不够只填写四种数字的,所以这样是矛盾的。所以,7是至少有一个了。
那么,这个结构删除的地方,就是所有7的交集。E1就是它们的交集。


 是咸鱼吖
是咸鱼吖

