关于柯西不等式和均值不等式,我一直以来都有三个疑惑,请大家指教,谢谢。
一、关于柯西不等式,其实是有两种结果的,如图:

但这两个不等式实际上不是等价的,除了极特殊的情况外,普通情况下两个不等式的右边是不相等的,即(ac+bd)^2不等于(ad+bd)^2. 这就带来了一个问题:在实际的应用中,我们到底应该选择哪一种?
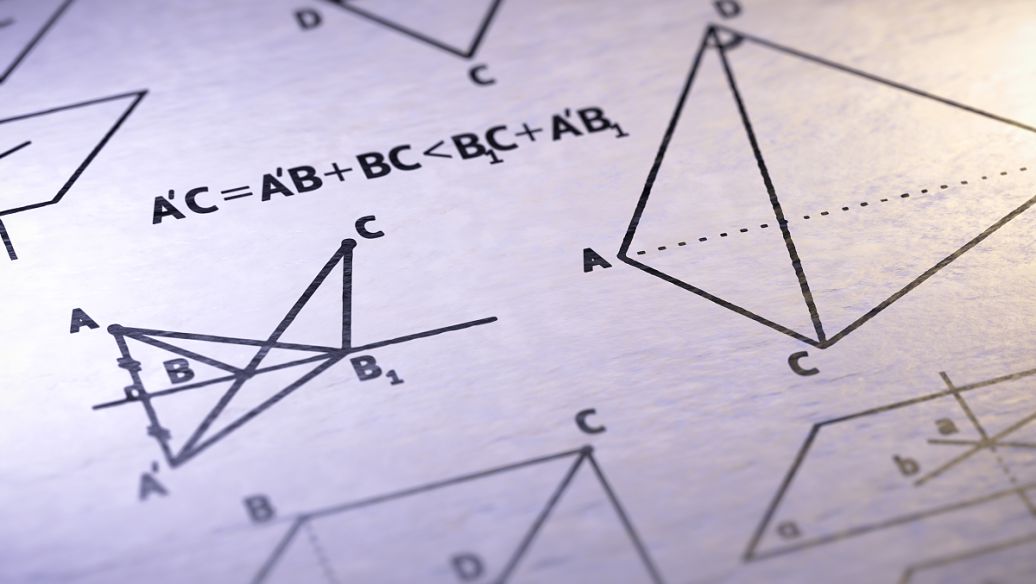
二、同样的,柯西不等式的三角形式也会出现两种结果,这两种结果同样不等价(除极特殊的情况),而且更为直观,如下图:

在实际解题中,我们应该怎么办,难道把两种结果都写出来?
三、还有一个均值不等式,当然运用均值不等式只会得出一个结果。虽然均值不等式是柯西不等式的推论,但均值不等式得出的结果却与上述的柯西不等式的两个结果都不相同。比如柯西不等式的三角形可用均值不等式(平方平均值不小于算术平均值)来计算,如下图:

也就是说,同一个题可能会出现三种不同的结果。怎么办?
如果有数值还比较好办,选范围较小的一个就行(是不是这样?);
但如果无法得到数值结果,而只是带着数值的代数式,那么,这三种解法所得出的不同结果,哪一个才是正确的呢?
这个已经困惑我很久了,不知道该怎么办呀。请大家指教。
我提的问题或许很粗浅,诚心请教,谢谢!
一、关于柯西不等式,其实是有两种结果的,如图:

但这两个不等式实际上不是等价的,除了极特殊的情况外,普通情况下两个不等式的右边是不相等的,即(ac+bd)^2不等于(ad+bd)^2. 这就带来了一个问题:在实际的应用中,我们到底应该选择哪一种?
二、同样的,柯西不等式的三角形式也会出现两种结果,这两种结果同样不等价(除极特殊的情况),而且更为直观,如下图:

在实际解题中,我们应该怎么办,难道把两种结果都写出来?
三、还有一个均值不等式,当然运用均值不等式只会得出一个结果。虽然均值不等式是柯西不等式的推论,但均值不等式得出的结果却与上述的柯西不等式的两个结果都不相同。比如柯西不等式的三角形可用均值不等式(平方平均值不小于算术平均值)来计算,如下图:

也就是说,同一个题可能会出现三种不同的结果。怎么办?
如果有数值还比较好办,选范围较小的一个就行(是不是这样?);
但如果无法得到数值结果,而只是带着数值的代数式,那么,这三种解法所得出的不同结果,哪一个才是正确的呢?
这个已经困惑我很久了,不知道该怎么办呀。请大家指教。
我提的问题或许很粗浅,诚心请教,谢谢!