数学吧 关注:901,295贴子:8,795,458
扫二维码下载贴吧客户端
下载贴吧APP
看高清直播、视频!
看高清直播、视频!
贴吧热议榜
- 1京东外卖能否撼动美团地位1587270
- 2鸣潮滑跪送上30抽朋友费1302100
- 3一人一句话评价下今天的库里1228248
- 4IG状态回暖轻松拿下WE1180629
- 5知音漫客疑似没打赢复活赛943046
- 6关税正在摧毁美国股市879050
- 7JDG麦哥被开后首战不敌WBG618720
- 8美团发文暗指京东才是大恶人489854
- 9我国试验的非核氢弹威力如何465740
- 10龙胖退隐男乒谁扛大旗386274



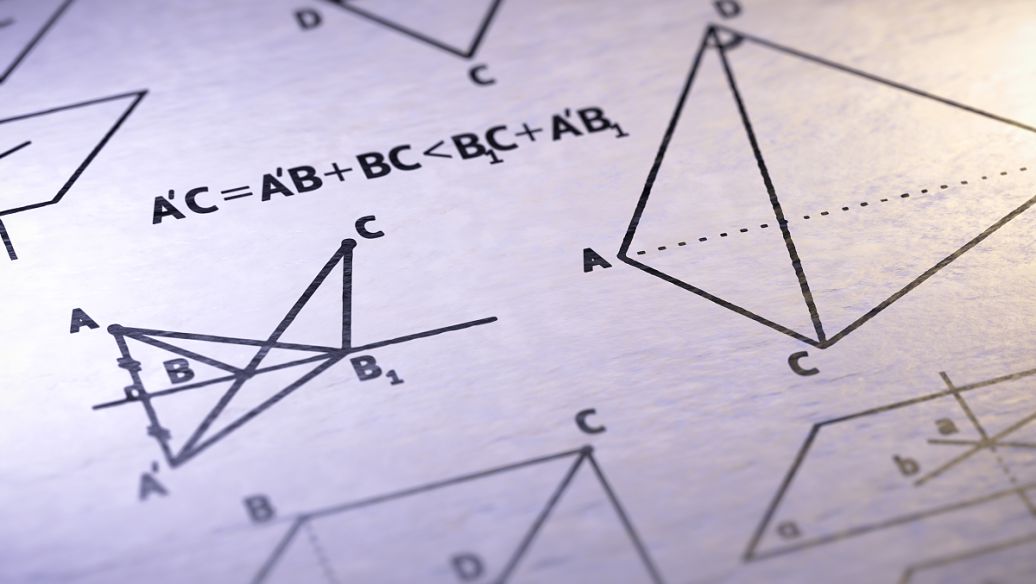




 有趣
有趣








